Chapitre 2

Vous trouvez ci-dessous toutes les solutions des activités, énigmes ou jeux du chapitre 2.

Page 43: Jeu d'entrée : une énigme arithmétique

Voici des exemples de solutions : (Il en existe d'autres)

• Exemple 1 : 36 = 4 · 12 - 2 · 6
• Exemple 2 : 60 = 2 · 15 + 3 · 10
• Exemple 3 : 16 = 12 + 2 + 6:3
• Exemple 4 : 11 = 2 · 4 + 1 · 3
• Exemple 5 : 0 = (12 - 9 - 3) · 6
• Exemple 6 : 7 = 18:2 - 16:8

Page 49: 0 et 1, un duo malin

Page 53: Un casse-tête

4 + 5 = 9

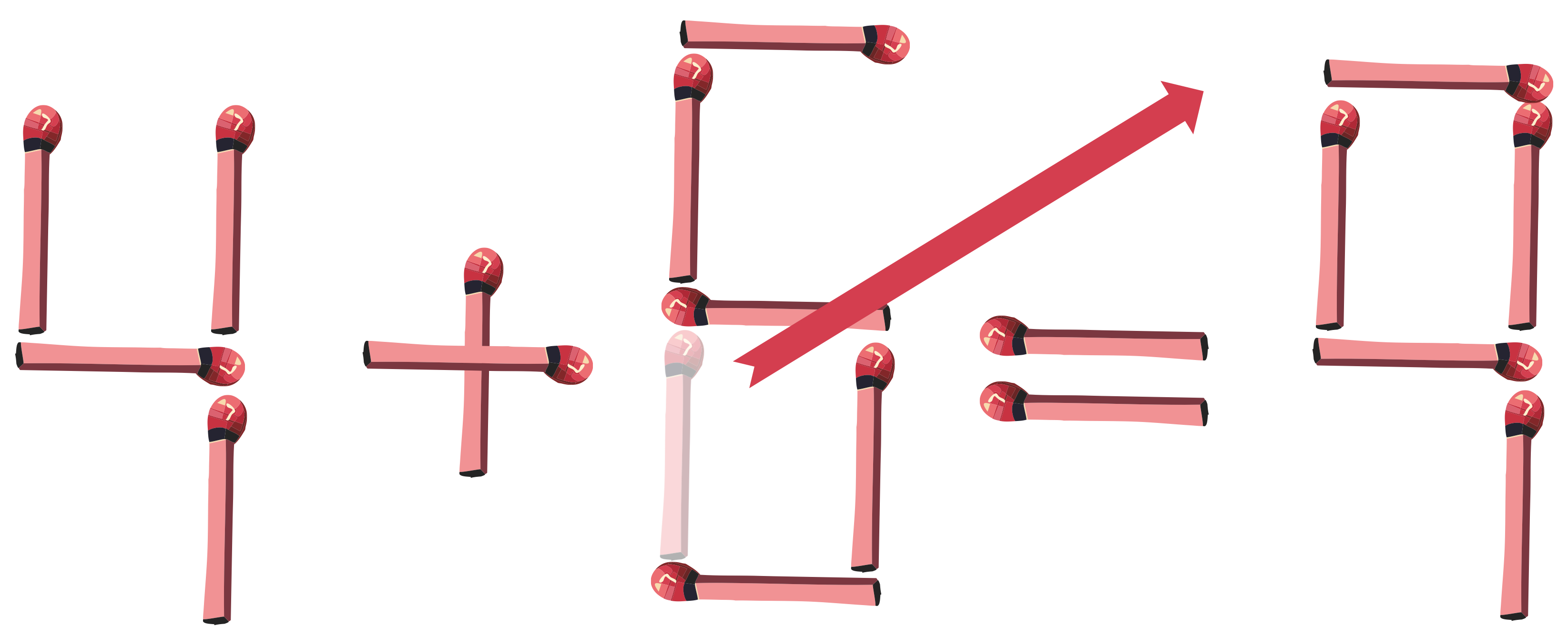
Autre solution : 4 + 0 = 4

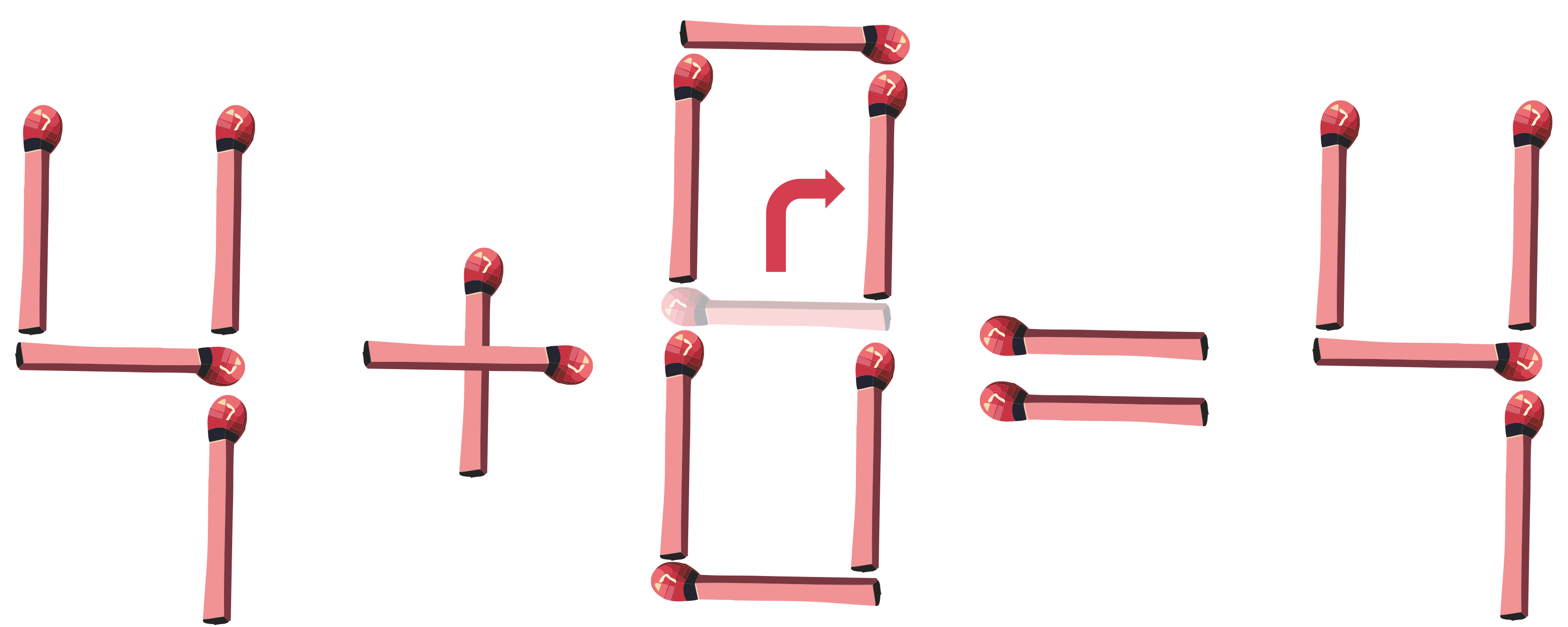
Page 54: Un phénomène : l'orage

• 1^ère méthode: Le son circule en 3 secondes de 3 · 0,337 m = 1 011 m ≈ 1km. En divisant par 3, on peut donc estimer que pour 1 seconde, le son circule d'un tiers de km.
• 2^e méthode: Au lieu de calculer 337 · 9 on se contente de l'approximation 300 · 9 = 2 700 m.

La première méthode donne une meilleure approximation.

Page 55: Le pliage d'une feuille

Faites le pliage !
Après un pliage, vous aurez deux épaisseurs, après 2 pliages 4, après 3 pliages 8, après 4 pliages 16 et après 5 pliages 32...

Nous avons donc doublé l'épaisseur par chaque pliage !

D'où la règle suivante : l'épaisseur sera égal à 2ⁿ avec n = nombre de pliages.

Pour n = 10, on aura donc 2¹⁰ épaisseurs de la feuille, donc 1 024.

Page 57: Une petite recherche

NON, car par exemple pour n = 41 on a 41² - 41 + 41 = 1681.

1 681 est donc divisible par 1, 41 et 1681.

Page 59: Un jeu : La course à 20 !

La recherche d‘une stratégie gagnante montre que le gagnant est celui qui dira 17, et avant 14, et avant 11, …, c‘est-à-dire que celui qui commence est sûr de gagner s‘il dit 2 (et s‘il sait jouer!).
On gagne si l'on choisit les nombres qui ont un reste 2 dans la division par 3.
En remplaçant 20 par 21 ou 22, on fait apparaître les différents restes dans la division par 3.

Page 63: Les maths en pratique : La clé USB

75 · 3 + 5 · 13 + 13 · 35 + 252 = 998. Il reste : 26 MB.

Page 64: À la découverte d'un tableur

• 1b: Voici les formules pour les différentes cases : D2: "=B2*C2" ; D3: "=B3*C3" ; D4: "=B4*C4" ; D6: "=SOMME(D2:D4)" ou bien "=D2+D3+D4"
• 2a: On doit modifier les quantités, donc les cellules C2, C3 et C4.
• 2b: 45 078 €

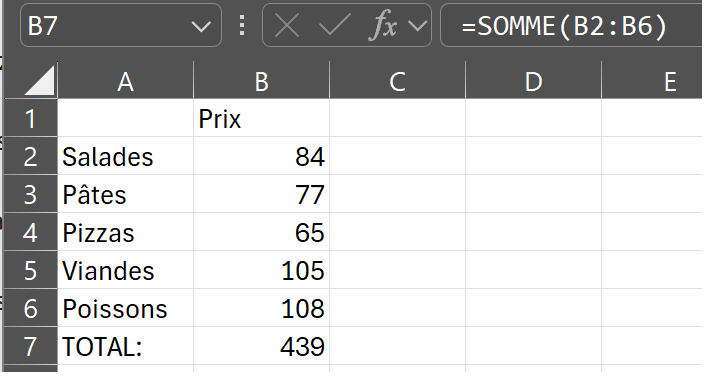
Page 65: Si vous étiez restaurateur

Il suffit d'écrire les catégories de plats dans une 1^ère colonne et les prix dans une 2^e colonne. En dessous des prix, ajouter le calcul de la somme totale, p.ex. : "=SOMME(B2:B6)" pour la case B7.

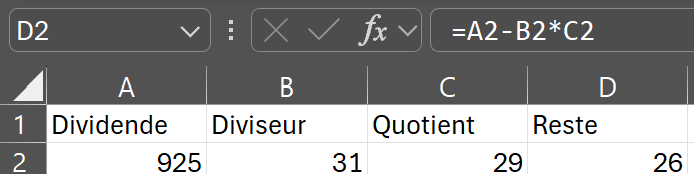
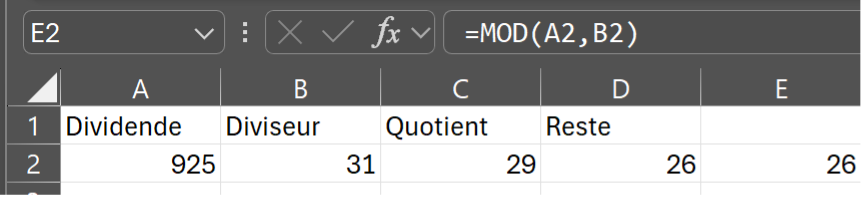
Page 65: Tableur et division euclidienne

Case D2: "=A2-B2*C2"

Page 71: Énigme : Vrai ou faux ?

Vrai car, 2 · 19 - 29 = 38 - 29 = 9 €.

Page 83: Les agendas de 2025 & 2031

Le système binaire

2¹⁰ = 1 024.