
Chapitre 8
Vous trouvez ci-dessous toutes les solutions des activités, énigmes ou jeux du chapitre 8.
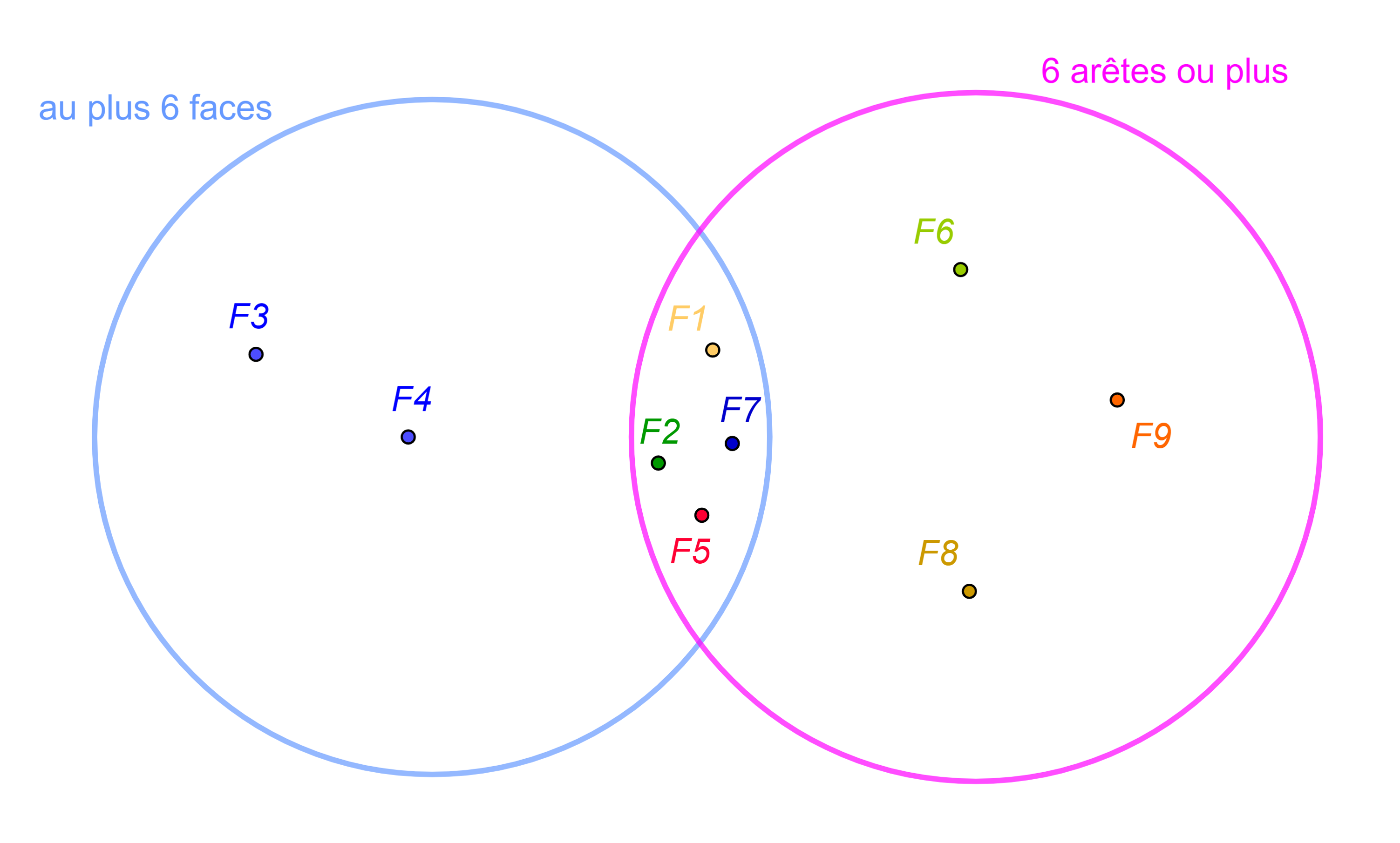
Page 275: Diagramme de Venn sur les formes 3D
Tableau récapitulatif :
| F1 | F2 | F3 | F4 | F5 | F6 | F7 | F8 | F9 | |
|---|---|---|---|---|---|---|---|---|---|
| Nombre de faces | 6 | 6 | 1 | 3 | 5 | 30 | 4 | 8 | 16 |
| Nombre d'arêtes | 12 | 12 | 0 | 2 | 9 | 84 | 6 | 18 | 42 |
Page 277: Les boîtes au quotidien
- Volume de la boîte : 873,8 cm3
- Volume (3 cm) : 1 066,5 cm3 ; Volume (4 cm) : 1 128,4 cm3 ; Volume (5 cm) : 1 083,5 cm3
- Hauteur qui donne le plus grand volume : 4 cm
Page 280-281: Activité - Relation d'Euler
- a.
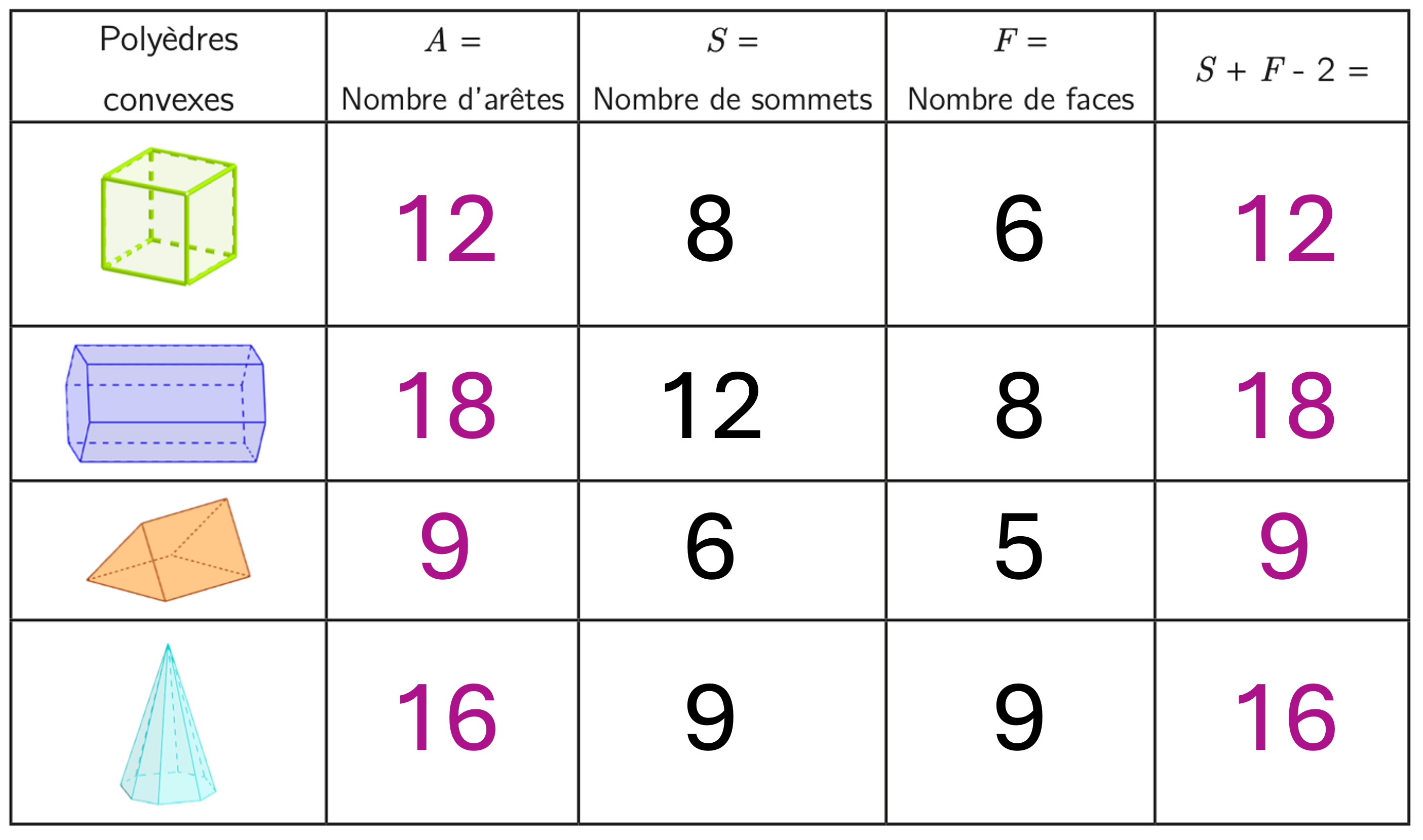
- b. On a la formule : A = S + F - 2.
Le tableau suggère que le nombre d'arêtes d'un polyèdre convexe est égal à la somme du nombre de sommets et de faces moins deux. Nous parlons de la relation d'Euler, nommée selon le mathématicien suisse Leonhard Euler (1707-1783) qui l'a introduite. Elle est vraie pour tout polyèdre convexe ainsi que pour quelques polyèdres non convexes « sans trou ».
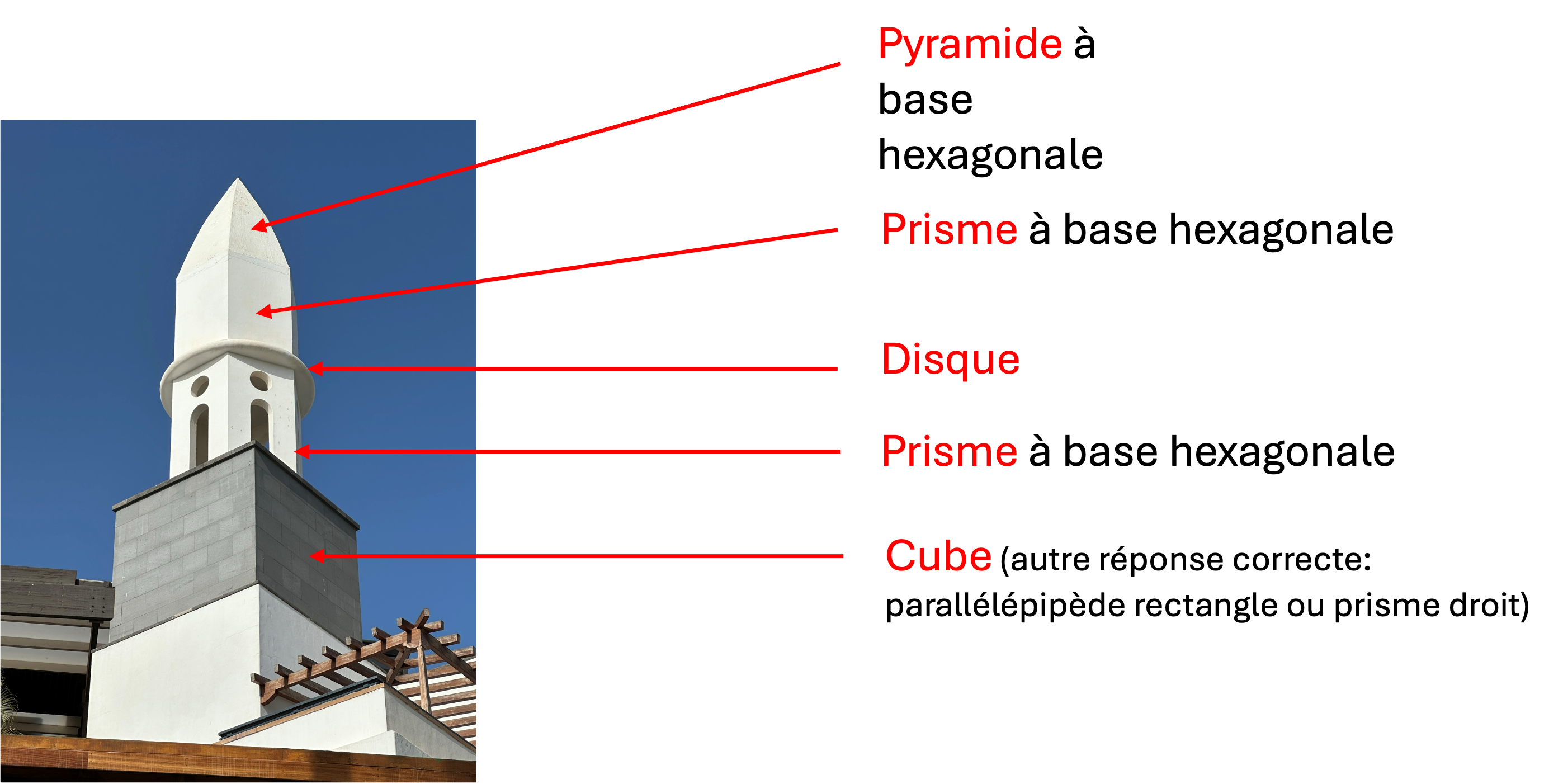
Page 281: Tour à Playa Blanca
Page 292: Tétracubes
Il existe huit tétracubes différents :
